Glossary

#algo

How do you notate a graph?#card §

A **graph **$G=(V,E)$ is a set of vertices $V(G)$, a set of edges $E(G)$, and a relation that associates two vertices via an edge.

Adjacent Nodes#card §

Two vertices $v$ and $w$ in graph $G$ are adjacent, denoted $v-w$, if there is an edge between them.

Incident#card §

If the vertex v is an endpoint of the edge e, then e and v are incident.

Degree#card §

The degree d(v) of a vertex v is the number of edges incident to it, counting loops twice.

Path#card §

A path is a trail in which neither vertices nor edges are repeated. A path is also a trail, thus it is also an open walk. The length of a path is the number of edges, or the sum of the weights of the edges. Here 6->8->3->1->2->4 is a Path

Complete Graph#card §

The complete graph is the graph (’$n$’ vertices) in which every pair of vertices are adjacent. Since each node is connected to every other node by an edge, each node has a degree of $n-1$ and there are $\frac{n(n-1)}{2}$ edges. 

Bipartite Graphs#card §

A bipartite graph, also called a bigraph, is a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent. This graph is bipartite because none of the red nodes connect to other nodes.

Adjacency Matrix#card §

The adjacency matrix $A$ of a graph G with $n$ vertices is the $n\times n$ matrix with rows and columns indexed by the vertices of $G$, where the number in the $i^{th}$ row and $j^{th}$ column of $A$ is the number of edges between the $i^{th}$ and $j^{th}$ vertex, counting loops twice.

Walk#card §

A walk is going from any node to another node, and is the most general definition of this process for a graph.

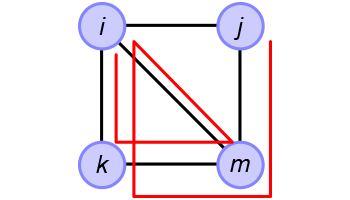
Trail#card §

A trail is a walk with no repeated edge.

Oath#card §

A oath is a walk with no repeated vertex.

Circuit#card §

A circuit is a trail whose first and last vertices are the same.

Cycle#card §

A cycle is a circuit with no repeated vertex other than the first and last vertex. 

Length#card §

The length of a walk, trail, path, circuit, or cycle in a graph is the number of edges in it (counting repeated edges multiple times).

Connected#card §

A graph G is connected if, for every pair of vertices in G, there exists a path between them.

Subgraph#card §

A subgraph H of a graph G is a graph such that V (H) is a subset of V (G) and E(H) is a subset of E(G).

Eulerian Circuit#card §

A Eulerian circuit of a graph G is a circuit which contains every edge of G.

Hamiltonian Cycle#card §

A Hamiltonian cycle of a graph G is a cycle which contains every vertex of G.

Neighbourhood#card §

The neighbourhood of a vertex v is the set of vertices adjacent to v.

Tree#card §

A tree is a connected graph with no cycles. 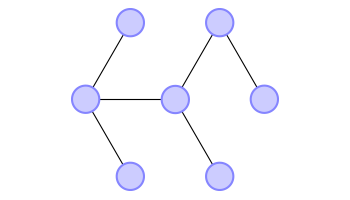In any tree, $|E|=|V|-1$

Order#card §

Number of vertices or nodes, $|V|$.

Size#card §

Number of edges of a graph, $|E|$

Leaf#card §

A leaf of a tree is a vertex of degree 1.

Spanning Subgraph#card §

A subgraph that is obtained only by edge deletions, so it therefore contains all the vertices of the original graph.

Distance#card §

The distance between two vertices v and w is the length of the shortest path between them.

Forest#card §

A forest is a graph with no cycles. (and it only wouldn’t be connected if there are multiple trees within the forest)

Diameter#card §

The longest shortest path from any node to another. This means that is the maximum distance to get from any node to another. The diameter here would be 3!

Radius#card §

The radius of a graph is the minimum distance you can take to get to any other node from a central node. For example, in this graph, C can get to any other node in 2 moves, so the radius would be 2. 

Eccentricity#card §

The eccentricity is of a vertex is the maximum distance between the vertex and any other vertex. Below is a graph with each node labelled with its eccentricity.

Digraph#card §

A directed graph, or digraph, is a graph where each edge has a direction. 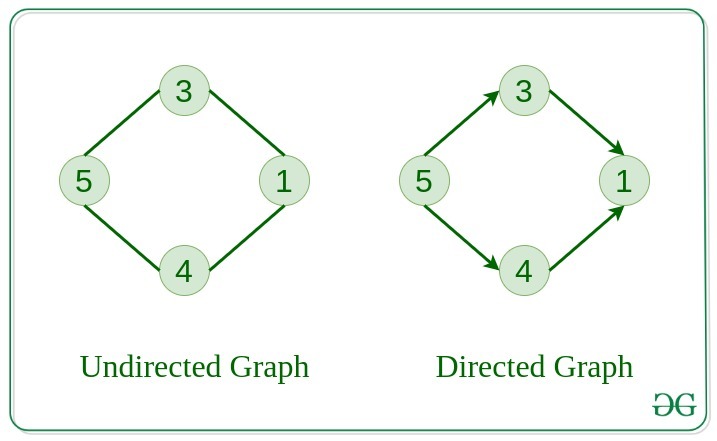A digraph is strongly connected if there is a directed path from every vertex to every other vertex in the graph.

DAGs#card §

A directed graph that is acyclic (contains no cycles) is known as a DAG. All trees are DAGs with the added restriction that each child only has one parent.

Algorithm#card §

An algorithm is a step-by-step process that describes how to solve a problem and/or complete a task, and which will always give the correct result.  Algorithms are often expressed using a loosely defined language called pseudocode, which is a hybrid language combining standard English with structures used in coding/programming languages.